Mathe Grundlagen - Klasse 10 - Realschulabschluss/mittlere Reife
Kernaussage: Eine kompakte übersichtliche Darstellung der Mathematik mit vielen Beispielen wird besser verstanden und erinnert (siehe auf Learn-Study-Work "Wie lernen - ohne zu vergessen?").
Übersicht
Es fängt ganz einfach an, weil es den Prüfungsteil ohne Taschenrechner gibt. Ich habe mir die Übungsaufgaben der Bundesländer für den Realschulabschluss angesehen und hier genau das Wissen aufgeführt, welches zum Lösen dieser Aufgaben notwendig ist. Vorteil: Man kann die Teilgebiete sehr schnell durchlesen und sieht, ob man alles verstanden hat.
Immer zuerst die Schlussfolgerung lesen. Ist diese bekannt, braucht die Erklärung nicht gelesen werden.
- Zahlenarten - Addition/Subtraktion - Multiplikation/Division - Brüche - Potenzen - Maßeinheiten umrechnen
- Prozentrechnung
- Kombinatorik
- Wahrscheinlichkeit
- Funktionen
Zahlenarten


Addition / Subtraktion
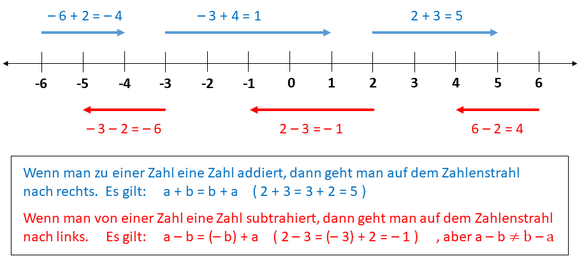
Klammern werden in der Mathematik zu verschiedenen Zwecken eingesetzt. Hier zeigen sie, welches Vorzeichen zu einer Zahl gehört und welche Operation zuerst ausgeführt werden soll:
Bei 6 - (2 + 3) soll zuerst 2 + 3 = 5 gerechnet werden und dann 6 - 5 = 1 .
Steht von einer Klammer ein Minuszeichen, muss man die Vorzeichen in der Klammer umkehren, wenn diese wegfallen soll: 6 - (2 + 3) = 6 - 2 - 3 = 1 .
Steht vor der Klammer ein Pluszeichen, werden die Vorzeichen nicht umgekehrt:
6 + (2 + 3) = 6 + 2 + 3 = 11 .
Beim Kopfrechnen ist es einfacher Zahlen zu zerlegen:
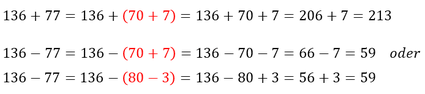
Schlussfolgerung: Mit dem Zahlenstrahl im Geiste die Größenordnung der Rechnung überprüfen. - Beim Auflösen einer Klammer mit negativem Vorzeichen, das Vorzeichen in der Klammer umkehren. - Beim Kopfrechnen schwierige Zahlen zerlegen.
Multiplikation / Division
Auch bei der Multiplikation ist es einfacher Zahlen zu zerlegen, wenn man im Kopf rechnen soll:
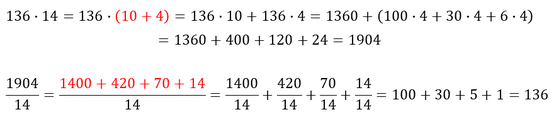
Beim Rechnen mit Dezimalzahlen muss das Komma an die richtige Stelle gesetzt werden:

Schlussfolgerung: Beim Rechnen mit Dezimalzahlen die Nachkommastellen abzählen und dies beim Ergebnis berücksichtigen. - Minus mal Minus gibt Plus. - Durch einen Bruch dividieren, indem man mit seinem Kehrwert multipliziert. - Brüche durch Kürzen vereinfachen.
Brüche
Brüche können nur addiert oder sustrahiert werden, wenn sie den gleichen Nenner haben. Deshalb müssen Brüche erweitert werden, was bedeutet, dass Zähler und Nenner mit der gleichen Zahl multipliziert werden. Das ist erlaubt, weil a/a = 1 und eine Multiplikation mit 1 verändert nicht den Wert des Bruches.
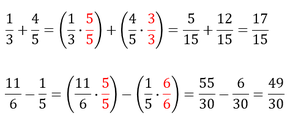
Schlussfolgerung: Brüche müssen auf den gleichen Nenner gebracht werden, bevor sie addiert oder substrahiert werden können.
Potenzen


Für die Addition/Subtraktion gibt es keine entsprechenden Regeln, da ist ein Vereinfachen nicht möglich.
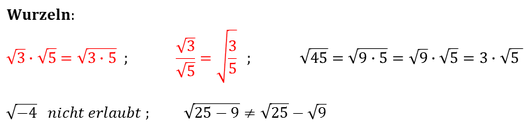
Schlussfolgerung: Exponent 0 → 1 - Exponent negativ → Bruch -
Exponent Bruch → Wurzel - Gleiche Basis: Multiplikation → Exponenten addieren, Dividion → Exponenten substrahieren - Gleicher Expoment: Multiplikation und Division → Basis zusammen in eine Klammer - Gleiche Wurzel: Multiplikation und Division → Basis zusammen unter die Wurzel - Unter einer Wurzel darf nichts Negatives stehen. - Bei einer Addition/Substraktion kann nichts vereinfacht werden.
Maßeinheiten umrechnen
Den Wert (mit Einheit), der umgerechnet werden soll, multipliziert man mit einem Bruch, der die gesuchte Einheit im Zähler und die zu verändernde Einheit im Nenner enthält und den Wert 1 hat. Dann kürzt sich die zu verändernde Einheit raus. Eine Multiplikation mit 1 ist erlaubt, weil sie den Ausgangswert nicht verändert.

Ich muss also immer wissen, wie die Grundeinheiten umgerechnet werden. Da sollte man diese Vorsilben im Kopf haben:
- milli - 1/1000
- centi - 1/100
- dezi - 1/10
- kilo - 1000
Gewicht: 1 g = 1000 mg ; 1 kg = 1000 g ; 1 Tonne = 1000 kg
Länge: 1 cm = 10 mm ; 1 dm = 10 cm ; 1 m = 100 cm ; 1 km = 1000 m
Fläche: Eine Fläche berechnet sich aus Länge x Länge.
1 cm2 = 100 mm2 = 10 mm x 10 mm ; 1 dm2 = 100 cm2 ;
1 m2 = 10000 cm2 = 100 cm ⋅ 100 cm ; 1 km2 = 1000000 m2 = 1000 m ⋅ 1000 m
Volumen: Ein Volumen berechnet sich aus Länge x Länge x Länge.
10 mm x 10 mm x 10 mm = 1000 mm3 = 1 cm3 = 1 ml
eine Packung Milch hat ungefähr:
10 cm x 10 cm x 10 cm = 1000 cm3 = 1 dm3 = 1000 ml = 1 Liter
100 cm x 100 cm x 100 cm = 1 m3 = 1000 Liter
Zeit: 60 s = 1 min, 60 min = 1 h (hour), 24 h = 1 d (day), 365 d = 1 a (year)
Schlussfolgerung: Den Wert (mit Einheit), der umgerechnet werden soll, multipliziert man mit einem Bruch, der die gesuchte Einheit im Zähler und die zu verändernde Einheit im Nenner enthält und den Wert 1 hat. - Die Umrechnung der Grundeinheiten und deren Vorsilben muss man auswendig lernen.
Prozentrechnung
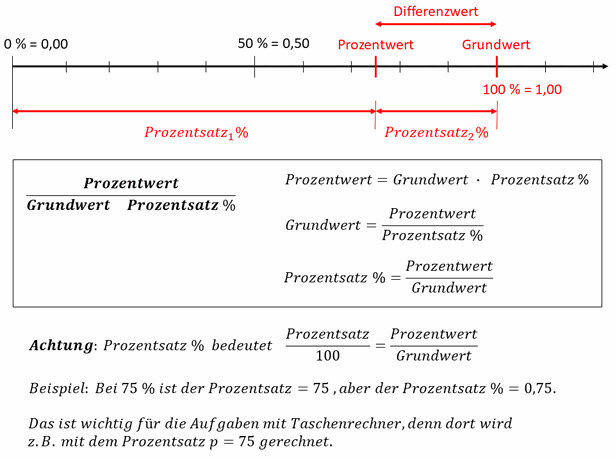
Bei der Prozentrechnung gibt es 5 Werte, nach denen gefragt werden kann:
Prozentwert, Grundwert, Prozentsatz 1, Prozentsatz 2 und nach dem Differenzwert zwischen dem Prozentwert und dem Grundwert. Wenn zwei Werte bekannt sind, können die anderen Werte berechnet werden.
75 % bedeutet 75 ⋅ 1/100 = 0,75 . Die 0,75 werden Prozentsatz % genannt. Zu unterscheiden davon ist der Prozentsatz p = 75. Dieses p wird in den Formeln der Prozentrechnung verwendet.
Beispiel: In einer Klasse sind 24 Schüler, von denen 75 % Rechtshänder sind. Der Anteil der Linkshänder beträgt 25 %, was 24 -18 = 6 Schülern entspricht.

Wie groß ist der Preisnachlass? Eine Sache kostet 500 Euro. Der Preis wird um 25 % reduziert. Der neue Preis ist 325 Euro. Er ist um 125 Euro reduziert worden.
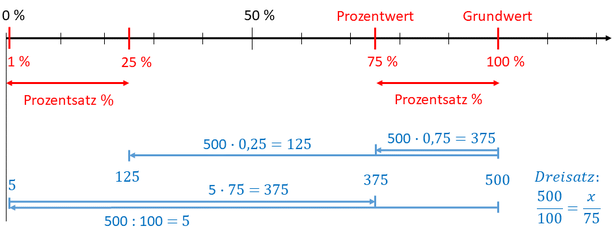
Im Kopf gerechnet: 500 x 0,75 = 1/2 x 1000 x 0,75 = 1/2 x 750 = 375 (Wenn ich mit 1000 rechne, dann mus ich das Ergebnis halbieren.), 500 - 375 = 125
Wie groß ist die Mehrwertsteuer? Eine Sache kostet netto 500 Euro. Der Preis mit Mehrwertsteuer soll berechnet werden.
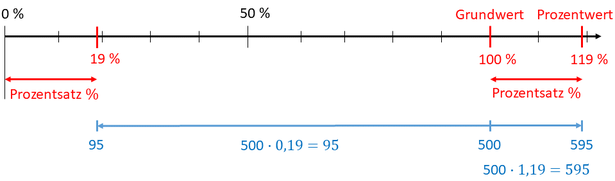
Im Kopf gerechnet: 500 ⋅ 1,19 = ½ ⋅ 1000 ⋅ 1,19 = ½ ⋅ 1190 = 595
,
500 ⋅ 0,19 = 500 ⋅ (2 ⋅ 0,1 - 0,01) = 500 ⋅ 2 ⋅ 0,1 - 500 ⋅ 0,01 = 2 ⋅ 50 - 5 = 100 - 5 = 95
(10 % von 500 sind 50, dann sind 2 ⋅ 10 % = 20 % = 100, um auf 19% zu kommen muss ich noch 1 % (= 5) abziehen).
Schlussfolgerung: Danach kann gefragt werden: Prozentwert, Grundwert, Prozentsatz des Prozentwertes, Prozentsatz der Veränderung und nach dem Differenzwert zwischen dem Prozentwert und dem Grundwert. - Sich zuerst selber fragen: Was ist der Grundwert? = Was ist 100 % ? - Die gesuchten Werte mit dem Dreieck "Prozentwert / Grundwert Prozentsatz %" berechnen. - Prozentsatz % ist z. B. 0,75.
Kombinatorik (Reihenfolgen)
Wenn es darum geht wie viele verschiedene Reihenhenfolgen es für die Anordnung von Objekten geht, dann ist diese Frage ein Teilgebiet der Kombinatorik. Für die Art der Reihenfolge gibt es vier Möglichkeiten:
- Reihenfolgen ohne Wiederholungen (ohne Zurücklegen im Urnen-Modell) - die Reihenfolge wird berücksichtigt
- Reihenfolgen mit Wiederholungen (mit Zurücklegen im Urnen-Modell) - die Reihenfolge wird berücksichtigt
- Reihenfolgen ohne Wiederholungen (ohne Zurücklegen) - die Reihenfolge wird nicht berücksichtigt
- Reihenfolgen mit Wiederholungen (ohne Zurücklegen) - die Reihenfolge wird nicht berücksichtigt
Reihenfolgen ohne Wiederholungen (ohne Zurücklegen)
1. Beispiel: Aus einer Urne mit 3 verschiedenen Kugel werden ohne Zurücklegen nacheinander 3 Kugeln herausgenommen (wie beim Lotto mit 6 Kugeln). Wie viele verschiedene Reihenfolgen sind möglich?
Für das erste Herausnehmen (Ziehung) gibt es 3 Möglichkeiten. Danach sind nur noch 2 Kugeln in der Urne übrig. Für die zweite Ziehung gibt es also nur noch 2 Möglichkeiten. Für die dritte Ziehung gibt es nur noch 1 Möglichkeit, weil sich jetzt nur noch eine Kugel in der Urne befindet.
Insgesamt gibt es 3 ⋅ 2 ⋅ 1 = 6 Möglichkeiten:

Das Bild (Baumdiagramm) zeigt, dass schon bei der 2. Ziehung 6 verschiedene Reihenfolgen möglich sind. Das erklärt sich dadurch, dass es bei der 3. Ziehung nur noch 1 Kugel in der Urne gibt und man hat keine Wahlmöglichkeit mehr hat.

2. Beispiel: 5 Personen stellen sich hintereinander auf (5 Personen und 5 "Ziehungen", n = 5 und k = 5).
Wie viele verschiedene Reihenfolgen sind möglich? 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 120
Allgemein: Eine Menge von n Elementen hat 1 ⋅ 2 ⋅ 3 ⋅ ... ⋅ n = n! Möglichkeiten von Reihenfolgen, wenn alle Elemente "gezogen" werden (n - k = 0). (Ohne Zurücklegen: Die Zahl, mit der bei jeder Ziehung multipliziertwerden muss, verringert sich jeweils um 1.)
3. Beispiel: Das obige Baumdiagramm zeigt 3 Ziehungen. Wieviel Möglichkeiten gibt dafür, dass die letzte gezogene Kugel blau ist? Das Diagramm zeigt, dass es 2 Möglichkeiten gibt: grb und rgb. Wie kann das allgemein berechnet werden? Die 3. Ziehung liegt fest (blaue Kugel), also können die ersten beiden Kugeln variieren. Für 2 Kugel und 2 Ziehungen (n - k = 0) gibt es n! = 2 ⋅1 = 2 Möglichkeiten.
Komplizierter: In der Urne gibt es 6 numerierte Kugel und es wird viermal gezogen. Wieviele Möglichkeiten gibt es, dass die vorletze Kugel die Zahlen 5 und die letzte Kugel die Zahl 6 hat? Da die letzten beiden Kugeln festliegen mit den Nummern 5 und 6, können nur bei den ersten beiden Ziehungen die Nummern 1, 2, 3 und 4 variieren.

Reihenfolgen mit Wiederholungen (mit Zurücklegen)
1. Beispiel: Aus einer Urne mit 3 verschiedenen Kugel wird 2 Mal mit Zurücklegen eine Kugel herausgenommen. Wie viele verschiedene Reihenfolgen sind möglich?
Für das erste Herausnehmen (Ziehung) gibt es 3 Möglichkeiten und für die zweite Ziehung auch 3 Möglichkeiten, weil die gezogene Kugel der ersten Ziehung
zurückgelegt wurde. Insgesamt gibt es 3 ⋅ 3 = 9 Möglichkeiten.

2. Beispiel: Es wird dreimal mit einem Würfel gewürfelt. Wie viele Reihenfolgen sind möglich? 6 ⋅ 6 ⋅ 6 = 216 (n = 6 ; K = 3)
Allgmein: Bei einer Menge von n Elemente gibt es bei k Ziehungen mit Zurücklegen
nk Möglichkeiten von Reihenfolgen. (Mit Zurücklegen: Die Zahl, mit der bei jeder Ziehung multipliziertwerden muss, bleibt immer gleich.).
Schlussfolgerung: 1. Frage: Geht es um Reihenfolgen mit oder ohne Wiederholungen? (mit oder ohne Zurücklegen?) - Das Baumdiagramm zeigt die möglichen Ergebnisse für jeden Durchgang (für jede Ziehung). -
Ohne Zurücklegen: Es gibt n! / (n - k)! Möglichkeiten. - (es gilt: 0! = 1)
Mit Zurücklegen: Es gibt nk Möglichkeiten. (n Elemente, k Ziehungen)
Um ein Baumdiagramm zu vereinfachen, können alle Zweige mit uninteressanten Ergebnissen zusammengefasst oder weggelassen werden.
Wahrscheinlichkeit
Funktionen
Für Funktionen siehe auf Learn-Study-Work bei "Mathematische Funktionen"
