Was ist Mathematik?

Kernaussage: Ich bin kein Mathematiker und kenne die höhere Mathematik nur wenig. Deshalb nutze ich passende Zitate und ziehe aus ihnen logische Schlussfolgerungen.

 

"Warum scheitern so viele Schülerinnen und Schüler, aber auch so viele Studierende, an der Mathematik? ... Mathematik ist schwierig. Sie ist abstrakt: das meiste davon ist nicht direkt mit Alltagserfahrungen oder -vorstellungen verbunden. Man hat nicht den Eindruck, dass sich die Mühe lohnt." (Loos, A., Ziegler (2016) G.M. "Was ist Mathematik" lernen und lehren. Math Semesterber 63, 155–169, S. 159, https://link.springer.com/article/10.1007/s00591-016-0167-y, 22.12.22)

 

"'Meist ist das ein Problem der Vermittlung', meint Jürgen Kramer, Professor für Mathematik und ihre Didaktik an der Humboldt-Universität in Berlin. ... 'Wenn Schüler und Schülerinnen sich mit Geometrie und Analysis beschäftigen müssen, dann wissen sie meist nicht, wofür das gut ist.'" (www.quarks.de/gesellschaft/bildung/mathematikunterricht-ist-das-wichtig-oder-kann-das-weg, 23.01.24)

 

Man sollte verstehen, was Mathematik ist, aber besonders auch, was die Mathematik will, wofür man sie benutzen kann. (Die Frage "Was will die Mathematik?" wird im dem folgenden Text noch nicht ausreichend beantwortet.)

 

"Für manche Fragen bieten mathematische Berechnungen sichere Prognosen für die Zukunft, für andere Fragen bietet sie Wahrscheinlichkeiten möglicher Antworten und für wieder andere gar keine Aussagen. ... Typische Aufgaben der Mathematik sind die Aufstellung von mathematischen Modellen und die Untersuchung ihrer Eigenschaften. Dazu gehört dann zum Beispiel das Lösen von Gleichungssystemen oder das Umformen von Gleichungen oder Formeln, wie wir es aus der Schule kennen. Typische Fragestellungen sind zum Beispiel ob ein gegebenes Gleichungssystem eine oder mehrere Lösung hat und wie gegebenenfalls eine Lösung gefunden oder angenähert bestimmt werden kann." (www.math.uni-magdeburg.de/~thein/teaching/analysis1/mathematik.pdf, 23.01.24, S. 1-2)

 

"Die Mathematik ist eine Formalwissenschaft, die aus der Untersuchung von geometrischen Figuren und dem Rechnen mit Zahlen entstand. Für Mathematik gibt es keine allgemein anerkannte Definition; heute wird sie üblicherweise als eine Wissenschaft beschrieben, die durch logische Definitionen selbstgeschaffene abstrakte Strukturen mittels der Logik auf ihre Eigenschaften und Muster untersucht." (https://de.wikipedia.org/wiki/Mathematik, 04.08.21, 2. Hervorhebung von mir)

 

"Ja, was ist Mathematik eigentlich? ... Wenn Sie die Gelegenheit haben, fragen Sie doch ein paar Mathematiker und Mathematikerinnen ... Sie werden ganz verschiedene Antworten bekommen. Beispielsweise 'Mathematik beschäftigt sich mit formalen Strukturen und quantitativen, d.h. durch Zahlen ausdrückbaren Beziehungen' oder 'Mathematik ist die Kunst, mit Hilfe exakten logischen Schließens aus bekannten Gegebenheiten neue, bislang unbekannte Wahrheiten zu entdecken'." (www.mathe-online.at/mathint/uema/i.html, 04.08.21, Hervorhebungen von mir)

 

Die entscheidenden Aussagen der beiden Zitate sind:

1. Mit Hilfe exakten logischen Schließens aus bekannten Gegebenheiten kommt die Mathematik zu neuen Erkenntnissen.
   
2. Die Mathematik beschäftigt sich mit selbstgeschaffenen abstrakten Strukturen und quantitativen Beziehungen.

Um diese Aussagen verstehen zu können, müssen mehrere Fragen beantwortet werden:

 

1. Wie kommt die Mathematik zu neuen Erkenntnissen?

 

Die Mathematik entstand aus der Untersuchung von geometrischen Figuren und dem Rechnen mit Zahlen (siehe Wikipedia-Zitat). Der Ursprung der Mathematik war also realitätsnah und nicht abstrakt.

 

"Zweifellos ist die Entwicklung der Mathematik in allen ihren Zweigen ursprünglich von praktischen Bedürfnissen und von Beobachtungen realer Dinge angeregt worden, selbst wenn dieser Zusammenhang im Unterricht und in der spezialisierten Forschung vergessen wird. Aber einmal begonnen unter dem Druck notwendiger Anwendungen, gewinnt eine mathematische Entwicklung ihren eigenen Schwung, der meistens weit über die Grenzen unmittelbarer Nützlichkeit hinausführt. ... Mit der Zeit schlug das Pendel nach der Seite der reinen Logik und Abstraktion aus, und zwar so weit, daß eine gefährliche Trennung der 'reinen' Mathematik von lebenswichtigen Anwendungsgebieten entstand." (https://link.springer.com/content/pdf/bfm:978-3-642-13701-3/1, 23.12.22, S. XVIV, XX)

 

Tatsächlich wird die Mathematik unterteilt in eine abstrakte reine und in eine realtitätsnahe angwandte Mathematik.

 

"Die Debatte des neunzehnten Jahrhunderts basiert auf einer unnatürlichen Einteilung in die klassische, reine Mathematik und die nützliche, angewandte Mathematik: eine Einteilung, die seit langem überwunden sein sollte." (https://link.springer.com/article/10.1007/s00591-016-0167-y, 22.12.22, S. 158)

 

Wie kam es zu der Unterscheidung? Es gibt zwei Möglichkeiten, neue Erkenntnissen zu gewinnen (siehe auf Learn-Study-Work "Was ist Wissenschaft?"):

 

1. Empirische Vorgehensweise (Induktion)

Wenn man aus der Beobachtung der Realität zu einer neuen Erkenntnis kommt, kann man diese in der Realität ausprobieren. Hat man damit Erfolg, dann wird die neue Erkenntnis als richtig angesehen, zumindest solange bis eine bessere Erkenntnis gefunden wurde.

 

2. Abstrakte Vorgehensweise (deduktives Schließen)

Wenn man von bekannten (oder selbst gesetzten) richtigen Vorrausetzungen/Erkenntnissen ausgeht, kann man durch logisches Schließen zu einer neuen Erkenntnis kommen. Die ist möglich, weil in der Realität logische Regeln gelten. Wer diese logischen Regeln für das Schließen anwendet, hat mit der neuen Erkenntnis in der Realität Erfolg.

 

Wer die Logik als von den Menschen "selbsterschaffen" ansieht, der konstruiert zwischen den beiden Vorgehensweise einen grundlegenden Unterschied. Wer daran glaubt, dass alle Erkenntnisse über die Realität aus der Realität kommen und sich in dieser beweisen müssen, der macht das nicht. "Wahre" Aussagen sind dann diejenigen, die in der Realität erfolgreich angewendet werden können.

 

"... wenn wir in einer unberechenbaren Welt leben würden, in der sich die Dinge zufällig oder auf sehr komplexe Weise änderten, wären wir nicht in der Lage, die Dinge zu verstehen. Wir leben aber in einem ... Universum, in dem sich die Dinge zwar ändern, aber nach Mustern, Regeln oder, wie wir sie nennen, nach Naturgesetzen. ... Und so wird es möglich, Dinge herauszufinden.". (Sagan, C. (2013). Cosmos. New York: Randon House Publishing Group, S. 41)

 

Die Logik der Menschen spiegelt die Logik der Natur (der Realität) wieder (meiner Meinung nach). Würde sich jemand für Theorien interessieren, die zwar logisch hergeleitet sind, sich aber in der Realität als falsch erweisen? Die Wissenschaftler würden versuchen, die Fehler in der Herleitung zu finden.

 

"Seit dem Ende des 19. Jahrhunderts, vereinzelt schon seit der Antike, wird die Mathematik in Form von Theorien präsentiert, die mit Aussagen beginnen, welche als wahr angesehen werden; daraus werden dann weitere wahre Aussagen [deduktiv] hergeleitet. Diese Herleitung geschieht dabei nach genau festgelegten Schlussregeln. Die Aussagen, mit denen die Theorie anfängt, nennt man Axiome, die daraus hergeleiteten [Aussagen] nennt man Sätze. Die Herleitung selbst ist ein Beweis des Satzes." (https://de.wikipedia.org/wiki/Mathematik, 07.08.21)

 

Wie entscheiden Mathematiker, ob eine Aussage wahr ist oder nicht?

 

"In unserer täglichen Kommunikation sind wir gewohnt Aussagen unterschiedlicher Verlässlichkeit zu machen. ... Nehmen wir beispielsweise die Aussage

Die Diagonale eines Rechtecks mit Seitenlängen 3 und 4 hat die Länge 5.

Sie zu beweisen ist eine einfache Anwendung des Satzes von Pythagoras ... und im Rahmen der Mathematik ... kommt ihr der Status einer wahren Aussage zu." (www.mathe-online.at/mathint/exakt/i.html, 25.12.22)

 

Der Satz des Phytagoras ist richtig, weil er mathematisch bewiesen ist und weil er täglich erfolgreich angewendet wird. (Phytagoras hat den Satz a² + b² = c² auch nicht "erschaffen", er hat ihn nur entdeckt. Der Satz galt schon bevor ihn jemand entdeckt hat.)

 

Der letzlich entscheidende Faktor für die Richtigkeit einer Aussage ist die Anwendung in der Realität. Aber da die menschliche Logik die Logik der Realität wiederspiegelt, sind auch logische Beweise Belege für die Richtigkeit. Die Nützlichkeit der Mathematik und die schöpferische Entdeckungsleistung der Mathematiker sollte immer betont werden (bei dem folgenden Zitat muss das Wort "Erfindung" durch das Wort "Entdeckung" ersetzt werden):

 

"... das Element der konstruktiven Erfindung, der schöpferischen Intuition [entzieht sich] einer einfachen philosophischen Formulierung; dennoch bleibt es der Kern jeder mathematischen Leistung, selbst auf den abstraktesten Gebieten. ... Der Lebensnerv der mathematischen Wissenschaft ist bedroht durch die Behauptung, Mathematik sei nichts anderes als ein System von Schlüssen aus Definitionen und Annahmen, die zwar in sich widerspruchsfrei sein müssen, sonst aber von der Willkur des Mathematikers geschaffen werden. Wäre das wahr, dann würde die Mathematik keinen intelligenten Menschen anziehen." (https://link.springer.com/content/pdf/bfm:978-3-642-13701-3/1, 23.12.22, S. XXI)

 

Viele Aussagen/Sätze der "reinen" Mathematik sind so weit fortgeschritten (s. o.), dass sich ihre Nützlichkeit noch nicht in der Realität gezeigt hat.

 

"Umgekehrt haben Mathematiker zuweilen Theorien entwickelt, die erst später überraschende praktische Anwendungen gefunden haben. So ist zum Beispiel die schon im 16. Jahrhundert entstandene Theorie der komplexen Zahlen zur mathematischen Darstellung des Elektromagnetismus inzwischen unerlässlich geworden. ... Des Weiteren galt die Beschäftigung mit der Zahlentheorie lange Zeit als intellektuelle Spielerei ohne praktischen Nutzen, ohne sie wären heute allerdings die moderne Kryptographie und ihre vielfältigen Anwendungen im Internet nicht denkbar." (https://de.wikipedia.org/wiki/Mathematik, 23.12.22)

 

Weil in unserem Universum logischen Regeln gelten, führt die Logik der Menschen zu richtigen Ergebnissen (s. u.). Wer das so sieht, ist von den praktischen Anwendungen nicht "überrascht".

 

"Reine Mathematik und angewandte Mathematik handeln beide von
Anwendungen, aber mit einem sehr unterschiedlichen Zeitrahmen. ... ein
Stück reine Mathematik schafft eine neue Idee oder eine Einsicht die, falls
sie gut ist, ziemlich wahrscheinlich zu einer Anwendung in zehn oder
zwanzig Jahren führen wird." (Vicente Muñoz and Ulf Persson, Interviews with three Fieldsmedalists (Andrei Okounkov, Terence Tao, and Wendelin
Werner). Notices of the AMS 54.3 (2007), 405–410)

 

Beispiel für logisches Schließen

n + (n + 1) + (n + 2) = 3n + 3 = 3(n + 1)

Wenn wir drei aufeinanderfolgende natürliche Zahlen addieren, dann dürfen wir schließen, dass wir das gleiche Ergebnis erhalten, wenn wir die erste Zahl mit 3 multiplizieren und dann die Zahl 3 addieren.

 

2. Was sind abstrakte Strukturen?

 

Eine Abstraktion ist ein Denkprozess, bei dem die Betrachterin das für sie Wesentliche eines Objektes oder einer Situation (bestehend aus mehreren Objekten) erkennt und so allgemein formuliert, dass es auch für andere Objekte oder Stuationen gelten kann. Sie beantwortet für sich die Frage: "Worauf kommt es an?"

 

Bei den Funktionalgleichungen handelt es sich "... um Abstraktionen, die Vielfältiges vereinheitlichen, damit den Überblick erleichtern und auch Antworten geben auf die Frage 'Worauf kommt es an?' ..." (https://dmg.tuwien.ac.at/winkler/pub/abstraktion.pdf, 25.12.22, S. 10)

 

"Beginnen wir mit einem Schulbeispiel, der Formel (a + b)² = a² + 2ab + b². ...

die Buchstaben in dieser Formel [sind] sogenannte Platzhalter, d.h. sie halten jeweils einen Platz frei. Wofür? Für bestimmte Zahlen, die man statt der Buchstaben einsetzen kann ... Was immer man für die Platzhalter a und b einsetzt, die Gleichung stimmt, denn es handelt sich um ein Gesetz für Addition und Multiplikation, und das ist der Witz der Gleichung, die mit Platzhaltern geschrieben ist. Sie drückt einen Zusammenhang aus, der für alle Zahlen gilt, weshalb man von den konkreten Zahlen abstrahieren und diesen Zusammenhang mit Buchstaben als Platzhaltern für alle möglichen Zahlen formulieren kann. Und das zeigt die Abstraktionstendenz der Mathematik ..." (https://www.uni-hannover.de/fileadmin/luh/content/alumni/unimagazin/2008_zahlen_globalisierung/08_1_2_6_8_hoynigen.pdf, 25.12.22, S. 6)

 

Abstrahieren lernen wir schon als Kleinkinder. Ein Kind, dass einmal von einem Hund gebissen wurde, wird von allen Tieren Abstand halten, die so ähnlich aussehen wie ein Hund.

 

Eine Struktur ist die "Anordnung der Teile eines Ganzen zueinander" (www.duden.de/rechtschreibung/Struktur, 26.12.22). Eine Struktur besteht also aus Objekten, die miteinander in Beziehung stehen.

 

"Durch die Jahrhunderte hatten die Mathematiker ihre Objekte, z. B. Zahlen,
Punkte usw., als "Dinge an sich" betrachtet. Da diese Objekte aber den Versuchen, sie angemessen zu definieren, von jeher getrotzt haben, dämmerte es den Mathematikern des 19. Jahrhunderts allmählich, daß die Frage nach der Bedeutung dieser Objekte als "wirkliche Dinge" für die Mathematik keinen Sinn hat - wenn sie überhaupt einen hat. Die einzigen sinnvollen Aussagen über sie beziehen sich nicht auf die dingliche Realität; sie betreffen nur die gegenseitigen Beziehungen zwischen undefinierten Objekten und die Regeln, die die Operationen mit ihnen beherrschen. Was Punkte, Linien, Zahlen "wirklich" sind, kann und braucht in der mathematischen Wissenschaft nicht erörtert zu werden. Worauf es ankommt und was "nachprüfbaren" Tatsachen entspricht, ist Struktur und Beziehung, etwa, daß zwei Punkte eine Gerade bestimmen, daß aus Zahlen nach gewissen Regeln andere Zahlen gebildet werden, usw." (https://link.springer.com/content/pdf/bfm:978-3-642-13701-3/1, 23.12.22, S. XXII)

 

Wie ist das gemeint? Wenn die Mathematiker nicht wenigsten die grobe Definition von "Punkten, Linien, Zahlen" kennen würden, könnten sie gar nicht über sie sprechen. Bei der Aussagenlogik allerdings geht es nur um die Beziehung zwischen den Aussagen.

 

"... in der Mathematik hat man ständig mit Aussagen zu tun. Um zu einer hinreichend formalen Betrachtungsweise zu gelangen, verlangt man aber, dass mathematische Aussagen stets entweder wahr oder falsch sind, weitere Möglichkeiten gibt es nicht. Dieses Prinzip bedeutet ... nicht, dass der Wahrheitswert einer mathematischen Aussage bekannt sein muss, es
bedeutet nicht einmal, dass der Wahrheitswert prinzipiell ermittelt werden
kann." (www.cis.lmu.de/~micha/kurse/matheI-WS0809/begleitmaterial/matheI_aussagenlogik.pdf , 25.12.22, S. 1-2)

 

Die Mathematiker bauen eine Struktur auf, indem sie die Aussagen ordnen.

 

"In einer ersten Annäherung besteht die Axiomatisierung darin, dass man in die Menge der Aussagen, die in einem bestimmten Gebiet gelten, Ordnung
bringt. Diese Ordnung besteht darin, dass man eine möglichst kleine Teilmenge aller dieser Aussagen isoliert, die die Eigenschaft hat, dass die anderen Aussagen aus ihnen logisch folgen ... Die Aussagen über das Gebiet fallen somit in zwei Klassen, einmal die Axiome und dann die Theoreme [Sätze], die man aus den Axiomen ableiten und damit beweisen kann. Die Axiome selbst lassen sich natürlich nicht beweisen, eben weil ein Beweis aus der Ableitung aus Axiomen besteht. ... Vielmehr ist die Frage jetzt, welche Theoreme man aus bestimmten Axiomen ableiten kann, wobei man die Axiome als gegeben voraussetzt. Zum Beispiel: Wenn für irgendwelche Objekte a und b und für die Operationen + und • die Rechenregeln der üblichen Addition und der üblichen Multiplikation gelten, dann kann ich die Formel (a + b)² = a² + 2ab + b² beweisen. ... Die Wahrheitsfrage für die Axiome selbst verschwindet; sie tritt erst bei der Konkretisierung eines Axiomensystems für eine bestimmte, z.B. physikalische Situation auf, aber das ist dann keine mathematische Frage." (https://www.uni-hannover.de/fileadmin/luh/content/alumni/unimagazin/2008_zahlen_globalisierung/08_1_2_6_8_hoynigen.pdf, 25.12.22, S. 7-8)

 

Nun gibt es zwei Arten von Mathematikern: Der eine Teil hat eine besondere Freude an dieser formalen (abstrakten) Arbeit, der andere betont die Nützlichkeit der Mathematik.

 

"Ein Mathematiker wie Klein, der ... seine Antrittsvorlesung in Leipzig „Über die Beziehungen der neueren Mathematik zu den Anwendungen“ gehalten hatte, wurde von seinen Kollegen schief angesehen, als er – als einziger deutscher Mathematikprofessor – 1895 Mitglied im Verein Deutscher Ingenieure wurde, trotz seiner theoretischen Arbeiten aus der Geometrie und Algebra, für die er zu dieser Zeit schon berühmt war.

Doch Klein verdanken wir zum Beispiel, dass heute in Gymnasien Funktionen, Differential- und Integralrechnung gelehrt werden ... , und er hat bis heute
Recht: Die angebliche Kluft zwischen Anwendung und Theorie erweist sich immer wieder als Phantom. Godfrey Harold Hardy etwa ist berühmt für sein Loblied auf die reine Mathematik, das er 1940 ... in seiner Apology sang ... Im selben Werk verstieg er sich sogar zur Behauptung „I have never done anything ’useful’“. ... In Wirklichkeit sind Teile der Arbeit Hardys heute sehr
nützlich, zum Beispiel, in der Verschlüsselung von Daten oder der Molekularbiologie (Hardy-Weinberg-Prinzip) etwa." (Loos, A., Sinn, R., & Ziegler, G. M. (2022). Panorama der Mathematik. Springer, Berlin, Heidelberg, S. 343-344)

 

3. Beschäftigt sich die Mathematik mit quantitativen Beziehungen?

 

"Am 11. Mai 1959 setzte der Physiker Eugene Paul Wigner ein inzwischen geflügeltes Wort in die Welt ... 'Das Wunder, dass die Sprache der Mathematik für die Formulierung physikalischer Gesetze so gut geeignet ist, ist ein wundervolles Geschenk, das wir weder verstehen noch verdienen.' Sicher ist: Bis heute rätseln Menschen über diese Fragen [317, 362]. Möglicherweise hat es etwas damit zu tun, dass Mathematik eben gar nicht so weltfremd und ideal ist, wie viele denken, sondern die Welt der Zahlen und ihrer Strukturen genau wie die physikalische Welt ... ganz einfach Teil der Realität sind, in der wir Menschen leben ..." (Loos, A., Sinn, R., & Ziegler, G. M. (2022). Panorama der Mathematik. Springer, Berlin, Heidelberg, S. 341-342)

 

"Mit Newton’s Philosophiae Naturalis Principia Mathematica, die 1687 veröffentlicht wurde, begann die Geschichte der Theoretischen Physik und der sich daraus entwickelnden mathematischen Naturwissenschaften mit dem Ziel einer quantitativen Beschreibung von Naturphänomenen auf der Basis exakter mathematischer Gesetzmäßigkeiten." (https://itp.uni-frankfurt.de/~luedde/Lecture/Mechanik/Intranet/Skript/MechanikSkript.pdf, 02.11.24, S. iii)

 

Warum passt die Mathematik so gut zu quantitativen Wissenschaften? Wie wir gesehen haben, hat die Mathematik zwei Seiten: Die angewandte Mathematik und die abstrakte logische Mathematik. Deshalb muss sie auch so definiert werden:

 

Definition: Die Mathematik ist eine Wissenschaft, die zwei Seiten hat: Zum einem macht sie Aussagen zu den quantitativen Beziehungen zwischen verschiedenen Objekten, zu anderen macht sie mit Hilfe der Logik Aussagen zu den Beziehungen zwischen den Elementen abstrakter Strukturen. (Was abstrakte Strukturen sind, wurde oben erklärt.)

 

Eine Definition darf keine Aufzählung sein (siehe auf Learn-Study-Work "Wie Wörter definieren"), aber wenn eine Sache zwei Seiten hat, muss das in der Definition gesagt werden.

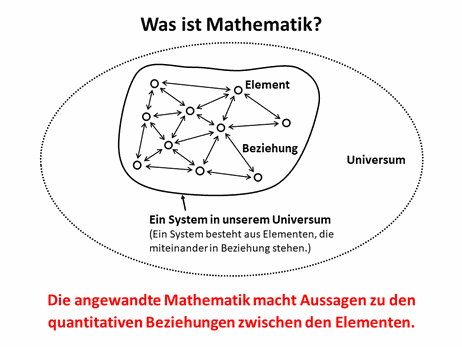
In den allermeisten Fällen geht es in der angewandten Mathematik um quantitative Aussagen. Es mag Bereiche geben, die sich mit rein qualitativen Aussagen beschäftigen. Für diese Fälle gilt "Ausnahmen bestätigen die Definition".

 

Beispiele:

Die Aussage: "In diesem Lager könnte es Reissäcke geben." ist eine qualitative Aussage und keine Mathematik. Zu einer mathematischen Aussage wird sie erst, wenn eine quantitative Angabe gemacht wird: "In dem Lager gibt es mindestens einen Reissack."

Wenn ich einen Kreis zeichne, dann ist das keine Mathematik. Dies ist es erst, wenn es um die Größe des Kreises geht.

 

Immer wenn es in den anderen Wissenschaften um quantitative Beziehungen geht, benötigen diese die Mathematik. So ist zum Beispiel die Formel: "Die Gewichtskraft F_G ist das Produkt aus der Masse m und der Erdbeschleunigung g" sowohl eine physikalische, als auch eine mathematische Formel.

 

Beispiel für einen Beweis:

Frage (Problem): Ist die Summe von drei aufeinanderfolgenden natürlichen Zahlen durch 3 teilbar?

Antwort und Beweis: Ja, denn n + (n + 1) + (n + 2) = 3n + 3 = 3(n + 1)

und 3(n + 1) ist für alle natürlichen Zahlen n durch 3 teilbar.

 

Eine kompakte übersichtliche Darstellung der Mathematik ist besser zu verstehen und auch besser zu erinnern (siehe auf Learn-Study-Work "Mathe Grundlagen - 10. Klasse/Realschulabschluss").

 

Diese beiden Videos zeigen die Seiten der Mathematik: www.youtube.com/watch?v=mxVDSdqJIZg

www.youtube.com/watch?v=1zudtkaEkHw, 16.10.21

 

Lesen Sie auf Learn-Study-Work: "Wie lernen?", "Wie studieren?", "Aktives Lernen", "Lernen in der Schule", "Wie Probleme lösen?", "Wie Wörter definieren", die "Gliederung" und "Einleitung" einer Bachelor- oder Masterarbeit

 

in English: "What is Respect?", "How to respond to disrespect?", "How to write a text", "How to define words", "What is Science?", "What is Health?", "How to solve problems", "What are scientific methods?"

en français: "Qu'est-ce que le respect ?", "Comment réagir à un comportement irrespectueux ?", "Comment écrire un texte ?"

en español: "¿Qué es el respeto?", "¿Como responder a la falta de respeto?"

हिंदी भाषा में: "सम्मान क्या है?", "अनादर का जवाब कैसे दें"