Was sind mathematische Funktionen und was muss man über sie wissen?

Kernaussage:

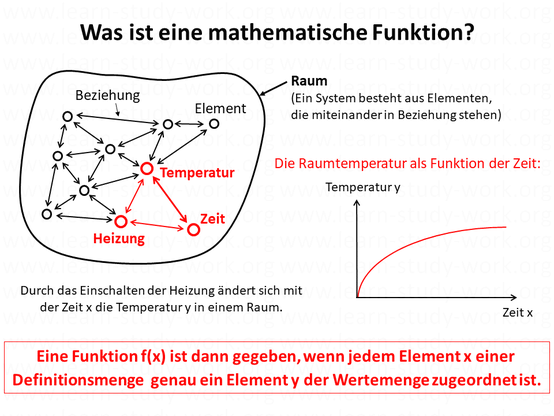
Was ist eine mathematische Funktion?

Alle Elemente unseres Universum stehen in Beziehung zu anderen Elementen. Es gibt kein Element, dass vollkommen isoliert existiert. Für viele Beziehungen sind mathematische Formeln bekannt, mit denen Werte berechnet werden können, die die Beziehung quantitativ beschreiben. Aber es gibt auch viele Beziehungen zwischen Elemente für die keine Formel bekannt ist oder für die eine Formel zu kompliziert wäre. So kann z. B. die Außentemperatur (für die Wettervorhersage) nur grob für wenige Tage berechnet werden.

"Immer dann, wenn der Wert einer Größe von dem Wert einer anderen Größe abhängt, liegt eine Funktion vor. Da die Natur voll von solchen Anhängigkeiten ist, kann eine unermesslich große Anzahl von Vorgängen und Zusammenhängen in der mathematischen Sprache der Funktionen beschrieben, modelliert und verstanden werden ... Betrachten Sie etwa ein Thermometer, dass an irgedeinem Ort hängt. ... Zu jedem gegebenen Zeitpunkt t ... wird eine bestimmte Temperatur T ... angezeigt. ... Jedem Zeitpunkt t ist eine Temperatur T zugeordnet. ... Ob sich die Temperatur aufgrund einer Theorie berechnen lässt oder ob sie abgelesen werden muss, ist dabei unerheblich - in jedem Fall handelt es sich um eine Funktion." (www.mathe-online.at/mathint/fun1/i.html, 14.08.21)

Bei einer Beziehung zwischen einem Zeitpunkt und der Temperatur fragt man sich also: "Wenn sich der Zeitpunkt verändert, wie ändert sich dann die Temperatur?" Weil sich beide ändern, werden Zeitpunkt und Temperatur als Variablen bezeichnet. Die Temperatur ist die abhängige Variable und der Zeitpunkt die unabhängige Variable (die Temperatur hängt vom Zeitpunkt ab).

Definition: Eine Funktion f(x) ist dann gegeben, wenn jedem Element x einer Definitionsmenge genau ein Element y einer Wertemenge zugeordnet ist.

Wenn die Definitionsmenge A und die Wertemenge B genannt wird, dann schreibt man für die Zuordnung, also für die Funktion f : A → B.

Wenn klar ist, was die Definitionsmenge und die Wertemenge sind, dann schreibt man vereinfacht: die Funktion y = f(x), wobei f die Zuordnung darstellt, f(x) den Funktionswert und y = f(x) die Funktionsgleichnug.

"Wenn klar ist, was A und B sind, oder wenn Definitions- und Zielmenge gerade nicht so wichtig sind, sprechen wir auch von „der Funktion y = f(x)“. Streng genommen ist dabei nur f die Funktion (Zuordnung), f(x) ist der Funktionswert an der Stelle x und y = f(x) ist die zugehörige Funktionsgleichung. Obwohl also „die Funktion y = f(x)" oder „die Funktion f(x)“ im heutigen Sinn nicht ganz präzise ist, werden wir diese eingängige und übliche Bezeichnung bewusst verwenden, weil sonst Formulierungen zwar vielleicht exakter, aber oft schwieriger und unverständlicher würden; es ist dann dem Kontext zu entnehmen, ob mit f(x) eine Funktion oder ein spezieller Funktionswert gemeint ist." (Humenberger, H., Schuppar, B. (2019) Mit Funktionen Zusammenhänge beschreiben. Springer Spektrum, Berlin, Heidelberg, S. 11)

Was sind mathematische Funktionen? Definition - jedem Element x wird ein Element y zugeornet - www.learn-study-work

Schon die frühen Mathematiker wussten, dass bei einem rechtwinkligen Dreick zwischen den Seiten eine Beziehung besteht und sie kannten die Formel, mit der man diese Abhängigkeit quantitativ berechnen kann: a² + b² = c²

Nun kann man sich fragen, wie verhält sich die Seite c, wenn die Seite b einen festen Wert hat und die Seite a verändert wird. Die Formel wird nach c aufgelöst:

Man sagt: Die untere Gleichung ist die Funktionsgleichung, mit der man zu jedem Wert von a einen Funktionswert c = f(a) berechnen kann. Jedem Wert von a wird so ein Wert c zugeordnet. Die Zuordnung geschieht, indem ein bestimmter Wert a in die Gleichung einsetzt und dann der zugeordnete Wert c ausgerechnet wird.

Nun musst noch festgelegt werden, welche Werte a einnehmen darf. Diese Werte werden Definitionsmenge genannt (z. B. gehört für die Funktion f(x) = 1/x der Wert 0 nicht zur Definitionmenge). Die zugeordneten Werte c werden Wertemenge genannt.

Eine Funktion kann als Wertetabelle dargestellt werden, die zeigt welche beiden Werte zueinander gehören. Wenn die Wertetabelle zu groß wird, ist es sinnvoll die Funktion zu visualisiern, indem man ihren Graphen (ihre zeichnerische Darstellung) in ein Koordinatensystem einträgt. Der Funktionsgraph ist die Menge aller Elementepaare (x│y), für die gilt y = f(x).

"Funktionsgleichung bzw. -vorschrift, Wertetabelle und Funktionsgraph stellen
die geläufigsten Darstellungsformen funktionaler Zusammenhänge dar. Zusätzlich gibt es noch die Darstellung über Pfeildiagramme und die verbale Beschreibung einer Funktion. Die einzelnen Darstellungsformen heben unterschiedliche Aspekte einer Funktion hervor. Während zum Beispiel die Wertetabelle eine eher statische Betrachtung vermittelt ... , bietet der Graph eine eher dynamische Sicht auf die Funktion an ..." (Meyer, M. (2021) Entdecken und Begründen im Mathematikunterricht. Springer Spektrum, Berlin, Heidelberg, S. 127)

Beispiel für eine verbale (sprachliche) Funktion aus der Steinzeit: Obwohl die Menschen damal noch keine Zahlen kannten, haben sie an jedem Abend überprüft, ob ihre Familie vollzählig ist. Das erhaltene Ergebnis stellt einen Funktionswert da.

Fortsetzung folgt ...